МФСП, 12 лекция (от 26 ноября)
Материал из eSyr's wiki.
(Различия между версиями)
(Новая: Докажем с применением индукции с помощью PVS, что марок номиналом 3 и 5 хватит, чтобы покрыть любую сумму...) |
м («МФСП, 13 лекция (от 26 ноября)» переименована в «МФСП, 12 лекция (от 26 ноября)») |
||
| (1 промежуточная версия не показана) | |||
| Строка 19: | Строка 19: | ||
По этому поводу будут 2 задачи: | По этому поводу будут 2 задачи: | ||
| - | # Написать формулу, получающуюся при решении задачи по методу Флойда | + | # Написать формулу, получающуюся при решении задачи по методу Флойда и показать, как она будет доказываться в PVS. |
| - | и показать, как она будет доказываться в PVS. | + | # Тоже на доказательство в PVS, скорее всего с применением индукции, но не сильно сложное. |
| - | # Тоже на доказательство в PVS, скорее всего с применением индукции, | + | |
| - | но не сильно сложное. | + | |
Следующая среда — консультация, через раз — коллоквиум. | Следующая среда — консультация, через раз — коллоквиум. | ||
Текущая версия
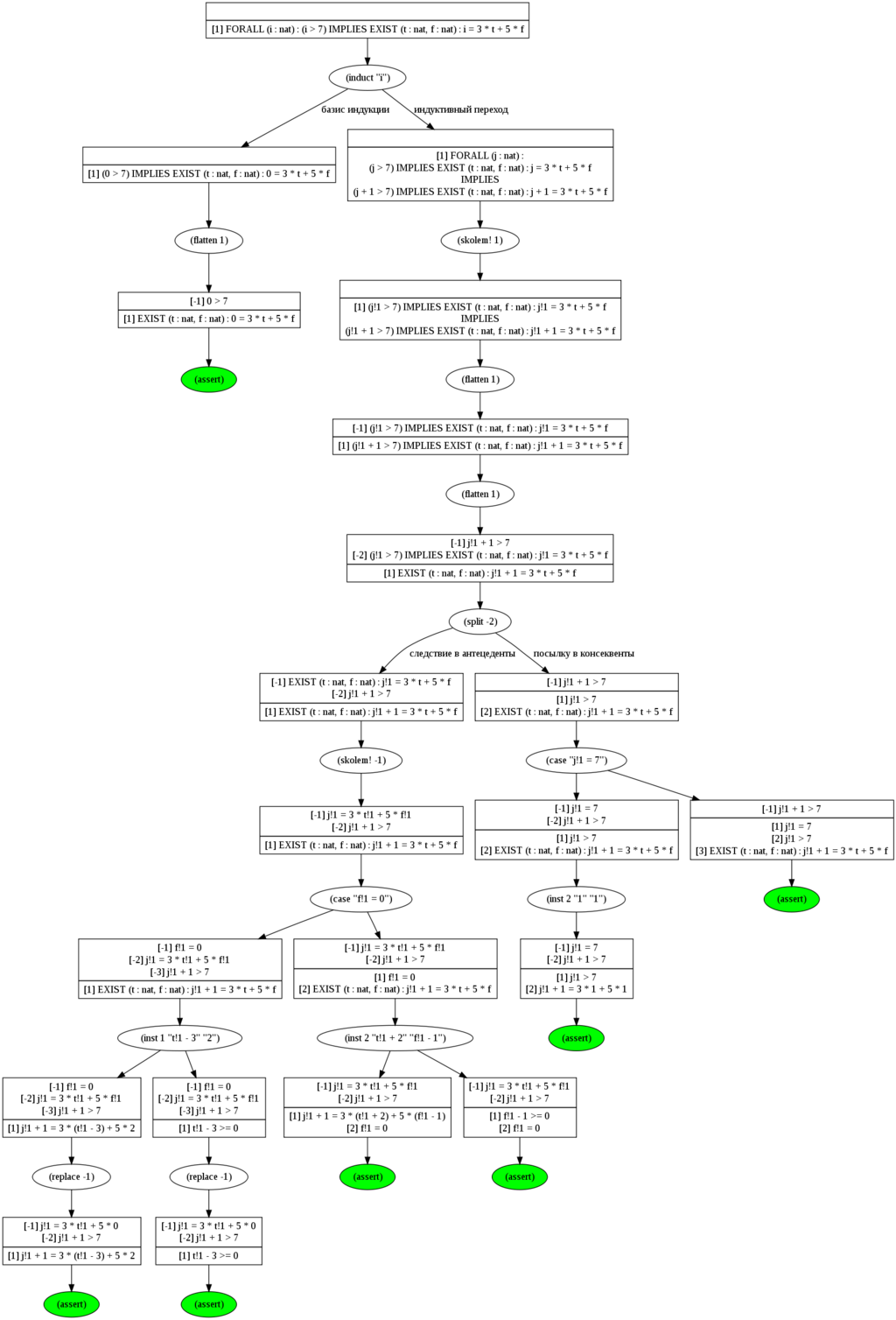
Докажем с применением индукции с помощью PVS, что марок номиналом 3 и 5 хватит, чтобы покрыть любую сумму, большую 7.
stamps : THEORY
BEGIN
stamps : LEMMA
(FORALL (i : nat) : (i > 7) IMPLIES
EXIST (t : nat, f : nat) :
i = 3 * t + 5 * f
)
END stamps
Сразу применять (skolem!) нельзя, так как мы хотим провести доказательство с использованием индукции. Следовательно, сначала применяем (induct "i"), а потом уже в индуктивном переходе применим (skolem!).
По этому поводу будут 2 задачи:
- Написать формулу, получающуюся при решении задачи по методу Флойда и показать, как она будет доказываться в PVS.
- Тоже на доказательство в PVS, скорее всего с применением индукции, но не сильно сложное.
Следующая среда — консультация, через раз — коллоквиум.
Ссылки:
Формальная спецификация и верификация программ
|
|
Эта статья является конспектом лекции.
Эта статья ещё не вычитана. Пожалуйста, вычитайте её и исправьте ошибки, если они есть.