МФСП, 03 лекция (от 17 сентября)
Материал из eSyr's wiki.
(брр) |
( —) |
||
| (3 промежуточные версии не показаны) | |||
| Строка 16: | Строка 16: | ||
Методика — вещь более размытая. Например, есть методика взятия интегралов? Вообще, есть, вас ей учили на первых курсах. | Методика — вещь более размытая. Например, есть методика взятия интегралов? Вообще, есть, вас ей учили на первых курсах. | ||
| - | Больше | + | Больше общих требований нет, и в реальной жизни методологий по построению программ, отвечающих всем трём позициям, нет. И то, что мы будем рассматривать, достаточно общие решения, но не нужно ждать от них фантастических результатов. |
VDM. Откуда растут корни? | VDM. Откуда растут корни? | ||
| Строка 28: | Строка 28: | ||
Рассмотрим пример. | Рассмотрим пример. | ||
| - | Мы уже не раз проходили, как устроена ОС, знаем, что процессы переходят из одних состояний в другие: например, iowait, пассивные. Это достаточно формальное определение, конечный автомат, и будем считать, что больше ничего нет. Микроядерная ОС (mm и pm) | + | Мы уже не раз проходили, как устроена ОС, знаем, что процессы переходят из одних состояний в другие: например, iowait, пассивные. Это достаточно формальное определение, конечный автомат, и будем считать, что больше ничего нет. Микроядерная ОС (mm и pm) — порядка 10 строчек на С. Как проверить соответствие? |
Например, проверить все переходы и состояния. Да, но этот подход недостаточно технологичный. Хотелось бы некое общее состояние получить. | Например, проверить все переходы и состояния. Да, но этот подход недостаточно технологичный. Хотелось бы некое общее состояние получить. | ||
| - | + | Общий подход следующий: мы разделяем два мира: мир моделей и реализаций. В модели и реализации, и там и там, есть своё пространство составляющих. Для простоты будем считать, что есть операции, функции, и данные берутся из входного пространства данных и данные генерируются в выходное пространство данных. Эти пространства разные. И в случае модели есть такая структура данных, пис. конечный автомат. В программе реализации такой может не быть. Там могут быть структуры существенно более богатые. И имеются операции. И тогда для проверки корректности рисуется такая диаграмма: имеется некоторое состояние, и мы в этом состоянии i_model мы применяем к нему переход f_модель и получаем результат j_model. И можем сделать соответствие i_impl →(f_impl) j_impl. Заметьте, что, собственно, входные данные не просто разные, но и в разных пространствах лежат. Между ними надо и можно установить соответствие. Соответствие устанавливается в эту сторону. Это некое отображение от сложного к простому. Часто это отображение называют абстракцией. Более принятое название — функция retrieve, retr. Коротко и красиво что можно сказать: реализация корректна в том и только в том случае, если диаграмма коммутативна. | |
| - | + | ||
| - | Общий подход следующий: мы разделяем два мира: мир моделей и реализаций. В модели и реализации, и там и там, есть своё пространство составляющих. Для простоты будем считать, что есть операции, функции, и данные берутся из входного пространства данных и данные генерируются в выходное пространство данных. Эти пространства разные. И в случае модели есть такая структура данных, пис. конечный автомат. В программе реализации такой может не быть. Там могут быть структуры существенно более богатые. И имеются операции. И тогда для проверки корректности рисуется такая диаграмма: имеется некоторое состояние, и мы в этом состоянии | + | |
Эта функция необязательно должна быть тотальная, у неё есть что-то типа предусловия. Это отображение (f) определено, когда некое предусловие удовлетворяется. Заметьте, что в реализации пространстве оно тоже может быть. И это должно быть согласовано. | Эта функция необязательно должна быть тотальная, у неё есть что-то типа предусловия. Это отображение (f) определено, когда некое предусловие удовлетворяется. Заметьте, что в реализации пространстве оно тоже может быть. И это должно быть согласовано. | ||
| Строка 40: | Строка 38: | ||
Для любого i в реализ. пространстве, если его retr удовлетворяет предусловию, то и оно сам должно ему удовлетворять. | Для любого i в реализ. пространстве, если его retr удовлетворяет предусловию, то и оно сам должно ему удовлетворять. | ||
| - | <math>\forall | + | <math>\forall i\_impl \isin i\_impl := pre\_model (retr(i\_impl)) \rArr pre\_impl (i\_impl)</math> |
Почему не выполняется в другую сторону: пример с логарифмом | Почему не выполняется в другую сторону: пример с логарифмом | ||
| - | Этот подход в общем смысле формален, | + | Этот подход в общем смысле формален, т.к.: предусловие может слаб. модель. По поводу постусловия обратная ситуация. |
По поводу результирующих функций | По поводу результирующих функций | ||
| Строка 52: | Строка 50: | ||
Сейчас мы заканчиваем с VDM, после этого перейдём к RAISE. | Сейчас мы заканчиваем с VDM, после этого перейдём к RAISE. | ||
| - | Что реально нужно делать, чтобы доказывать корректность программ: RAISE очень похож | + | Что реально нужно делать, чтобы доказывать корректность программ: RAISE очень похож на VDM. Спец. опис. реальным, рзм или имплицитным. Retr представляется как обычная функция, и потом просто нужно уметь доказывать, что два retr выполняются. |
Был выдвинут тезис, что модель и retr должны быть адекватны, и это правильно. Но с другой стороны, если модель большая, то приходится сильнее абстрагироваться. | Был выдвинут тезис, что модель и retr должны быть адекватны, и это правильно. Но с другой стороны, если модель большая, то приходится сильнее абстрагироваться. | ||
| - | Основная | + | Основная сложность — в функции retr. Сложность retr фактически сложность реализации. Поэтому подход другой: строится цепочка моделей. Для компиляторов было порядка 5 или 6 этапов. |
При помощи VDM верифицировали компилятор Ada. | При помощи VDM верифицировали компилятор Ada. | ||
| Строка 62: | Строка 60: | ||
Многие противники подхода говорили: вместо того, чтобы сделать работу честно и правильно 1 раз, необходимо сделать её несколько раз, провести работу по доказательству (которая очень трудоёмкая). Но опыт показал, что на компиляторах сроки разработки удаётся сократить и удаётся предъявить корректную программу с первого предъявления. | Многие противники подхода говорили: вместо того, чтобы сделать работу честно и правильно 1 раз, необходимо сделать её несколько раз, провести работу по доказательству (которая очень трудоёмкая). Но опыт показал, что на компиляторах сроки разработки удаётся сократить и удаётся предъявить корректную программу с первого предъявления. | ||
| - | Товарищи, которые | + | Товарищи, которые разработали VDM... RAISE расшифровывается как строгий подход к программной инженерии (rational approach to software engineering). Чтобы этим требованиям удовлетворять, самую сложную технологическую деталь в технологии VDM решили убрать — retr. Чем retr был хорош? Можно было изменять сигнатуру функции. VDM всё это разрешал, а RAISE запретил. что осталось? остался подход пошаговой детализации. Поскльку retr убрали, то сигнатуры модели и реализации совпали, структуры данных по существу одни и те же, т.к. что всё сильно упростилось, но при этом raise отошёл на ещё один шаг назад. Что было в VDM? Пусть в VDM первая модель — эксплицитная функция. При этом структуры данных должны быть описаны и заданы. В случае с нашим конечным автоматом разработчик может уже задуматься, как хранить состояние. Разработчики сказали, что на первом этапе модель должна быть предельно абстрактной. Функции есть, структур нет. И этот способ описания поведения системы, когда сигнатуры операций задаются, стр. не задаются, называют аксиоматической или алгебраической спецификацией. Есть тонкости в трактовке (кс и алг), но для нас разницы нет. В RAISE были введены аксиомы и при помощи них это опис. |
| - | И при | + | И при помощи RAISE может расписать достаточно детально: |
Из чего состоит технология RAISE: пис. модель нулевого уровня. Что должно быть задано? | Из чего состоит технология RAISE: пис. модель нулевого уровня. Что должно быть задано? | ||
| - | 0.1 Определяются некие типы данных. Не | + | 0.1 Определяются некие типы данных. Не описываются, а просто объявляются. |
| - | 0.2 Описываются | + | 0.2 Описываются сигнатуры операций (функций). Это значит, во-первых, задаётся имя функции и перечисляются типы операндов и результата (входных и выходных данных) |
| - | 0.2.1 С точки зрения RAISE, константы это | + | 0.2.1 С точки зрения RAISE, константы это такая функция без значений |
| - | Они | + | Они указывают, что функция тотальна, детерминирована и терминирующ. Если функция нетотальная, то надо писать тильду. На уровне сигнатур в чём нетотальность определить нельзя, надо смотреть сигнатуру |
0.3 Аксиомы. | 0.3 Аксиомы. | ||
Следующий шаг | Следующий шаг | ||
| - | 1.1 Типы данных | + | 1.1 Типы данных можно пополнить. |
1.2 Можно пополнить набор функций. | 1.2 Можно пополнить набор функций. | ||
| - | 1.3 Можно пополнить набор аксиом. Но все старые аксимы | + | 1.3 Можно пополнить набор аксиом. Но все старые аксимы сохранятся. |
| - | 1.4 | + | 1.4 Доказательство согласованности. |
| - | Модели 0 и 1 уровня должны быть согласованы. Как это делается. | + | Модели 0 и 1 уровня должны быть согласованы. Как это делается. Согласованность с позиции RSL термин неформальный, а технология RAISE ... расматривается отношение уточнения, дана модель мдет уточн. другую, и мы можем считать что модель 1 уточняет модель 0, если одна уточняет другую. И уточняет, если всё сохраняется и добавлено только новое, и есть один нюанс, связанный с уточнением самих типов данных. До этого типы данных были представлены только именами, по мере того, как прибл. к реализации, мы в какой-то момент, не обязательно для всех типов одновременно, должны эти типы определить (списки, деревья....) переходят объявления к определению можно делать два раза, не более чем. Первый раз — берётся и пис. реальная структура (например T3 — натуральное число или T4 — список натуральных чисел). Могу уточнить (T4 — конечный список натуральных чисел). Это первое уточнение типа. Второй вид: для каждой стр. данных форм. определяется т. н. максимальный тип. Это некий тип., пр. природу. Для булевских чисел максимальных. типов вл. сами булевские числа. Для натуральных — целые. Для конечных списков, множеств, тобр — бесконечн. Если есть список натуральных чисел, то вопрос, что будет максимальным типом стр. данных, гр. список натуральных чисел? Бесконечный список целых чисел. Такое уточнение — максимизация — тоже правильное уточнение. Самое главное, что нужно доказать — все аксиомы сохраняются. |
| - | Техника доказательства достаточно простая и | + | Техника доказательства достаточно простая и очевидная, как правило, подстановка. Дост.ю просто делать, если была аксиматическая спецификация, а в модели 1 написали определение. Помимо подст. исп. библиотек правил вывода, а она связ. с теориями, пстр. для типовых структур данных. Например: в случае множеств в теории сказано, что x ∈ {} всегда тождественно равно false. И при помощи последнего упрощения должны прийти к тому, что либо все аксиомы тождественно true, либо где-то не true, и вы доказали, что новая спецификация не является строгим уточнением исходной. В этом и состоит метод. |
| - | Пример: полностью пример имеется в | + | Пример: полностью пример имеется в методическом пособии. |
Имеется схем, пис. БД | Имеется схем, пис. БД | ||
| Строка 96: | Строка 94: | ||
'''axiom''' ∀ k : Key: - defined(K, empty) = false | '''axiom''' ∀ k : Key: - defined(K, empty) = false | ||
| - | Других ксим | + | Других ксим рассматривать не будем. |
| - | Эт | + | Эт нулевой уровень спецификации на первом обязаны пост. все спец. сигн, но БД, например, будет уточнена |
'''type''' Database = (Key × Data) - set | '''type''' Database = (Key × Data) - set | ||
| Строка 105: | Строка 103: | ||
defined()k,db = ∃ d : Data :- (k, d) ∈ db) | defined()k,db = ∃ d : Data :- (k, d) ∈ db) | ||
| - | Проверяем. Все типы данных определены, все сигнатуры пр. Для одного типа данных сказали, что это мн-во пар, и для двух функций сказали, | + | Проверяем. Все типы данных определены, все сигнатуры пр. Для одного типа данных сказали, что это мн-во пар, и для двух функций сказали, что empty всегда даёт пустое множество, и функция defined определена таким утверждением. Этого достаточно, чтобы рассуждать о сохранении или несохранении аксиомы. Для того, чтобы это делать, есть некая техника. В простом случае мы просто раскрываем все кванторы. |
| - | Раскрываем ∀, defined, empty, | + | Раскрываем ∀, defined, empty, потом раскручиваем квантор существования и мы приходим к некоторому выражению: (k, d) ∈ {}. Мы знаем, что это false, это означает, что левая часть тождественно false, значит, аксиома тождественно true. Вот мы провели доказательство, что первая аксиома сохранилась. |
| - | Практик-еор сообр: как в общем | + | Практик-еор сообр: как в общем случае проверять? общего ответа нет. Какие вообще спец. включать, а какие нет? В общем случае ответа на этот вопрос нет. Практический подход такой: в наших функциях мы делаем первое грубое разделение: какие функции сзд. новые данные в нашей системе (тут мы уже разделяем целевые объекты и вспомогательные). Те операции, где мы получаем новое состояние БД, это т.н. функции-генераторы, генераторы новых значений целевого типа. Те функции, которые позволяют узнать только некоторые характеристики, это некие обсерверы, которые позволяют что-то узнать (напр, lookup). Эти функции на состояние БД не влияют. И есть ещё более тонкое деление: функция remove. Любое значение Database мною построено при помощи цепочки инсертов, и для генерации всех значений БД куьщму не нужна, а а в реальной жизни нужна и в модели должна присутствовать. Эти функции, которые несут некоторую избыточность, их называют трансформерами или модификаторами. Они меняют состояние, но они приводят к состояниям, к которым можно без них перейти. |
| - | В число | + | В число аксиом системы обычно включают аксиомы, описывающие генераторы и обсерверы. А после того, как отработал генератор или трансформер, как изменилось поведение системы? А это даёт обсервера. И если для комбинаторной генерации и обс. есть опис. поведение, то это даёт эффект генератора. Т.о., мы должны согласовать с лектором, это самое абсолютное описание системы, которое может быть. |
| - | Теперь грустном: на | + | Теперь грустном: на экзамене будет задача, на которой необходимо будет доказать правильности или неправильность уточнения. |
| - | По поводу реальной жизни: | + | По поводу реальной жизни: никакие подобные системы аналитически не заказываются, на отдельные подсистемы техника доказательства используется в RAISE. Тематика становится всё более востребованной. |
{{МФСП}} | {{МФСП}} | ||
{{Lection-stub}} | {{Lection-stub}} | ||
Текущая версия
Корректность программ
Тема сегодняшней лекции: определение корректной программы и рассмотрение двух методов, которые призваны выдавать программы, корректные по построению
Два метода: VDM и RAISE (этому методу посвящена 6 глава)
Что мы ожидаем от методов построения программ:
- Он должен быть… это может быть максималистское требование… не все из них выполняются на 100 процентов… применим на практике. Понятно, что классов задач много разных, и если он применим к данному классу, то не факт, что применим к другому
- Строгий. Что это означает? Можно достаточно чётко сформулировать границы его применения, и в зависимости от того, какая задача стоит, ответить, имеет смысл применять метод или нет. Во-вторых, те гарантии, которые метод предоставляет, должны выглядеть достаточно убедительно — не общие утверждения
- Должен быть достаточно технологичным. Вот зубы лечат — это технология? Да, во всём мире учат именно технологии, есть чёткий регламент, чёткая последовательность, что надо сделать. Если врач выходит за рамки технологической цепочки, его почти всегда тут же застрахуют и, может быть, лишат лицензии. Сначала анализ, потом осмотр и так далее. Всё расписано достаточно подробно, и любого студента медицинского вуза каждому шагу в этой технологии можно обучить.
Вопрос: чем отличается от методики:
Методика — вещь более размытая. Например, есть методика взятия интегралов? Вообще, есть, вас ей учили на первых курсах.
Больше общих требований нет, и в реальной жизни методологий по построению программ, отвечающих всем трём позициям, нет. И то, что мы будем рассматривать, достаточно общие решения, но не нужно ждать от них фантастических результатов.
VDM. Откуда растут корни?
Середина 60х годов. Примерно этот период. IBM объявило и появились первые серии Series 360. Это был первый масштабный проект, где объявлялась унифицированная серия машин с унифицированным набором команд. За счёт унификации, с одной стороны, выходила огромная экономия, с другой стороны, требования ко всему были очень высокие, так же как и требования к компилятору. Вместо всех языков программирования тогда были Fortran, Cobol, Assembler. Вместо этой тройки был предложен PL/1. но должен был изменить собой вообще всё. То есть, ПО это ОС, компилятор и набор ПО, если нужно. И хотелось разр. этот самый главный в мире язык программирования т.к, чтобы он был правильный. ни не поленились и организовали лабораторию в Вене (?? V). Они изобрели VDL, Vienna Definition Language, на этом языке написали PL/1 и это описание вложили в компилятор. Это описание был сделано, опубликовано. Не полностью, примерно 95%. После этого творческому коллективу дали паузу, на пересмотр творческого решения и проблемы, и они предложили VDM, Vienna Developer Method. Когда разработали VDL, на технологичность не обращали внимания. Если написан язык и систем команд компьютера, то теоретически можно на вход программе их подать и получить на выходе компилятор. Эта задача есть и сейчас, но в таком максимальном варианте не решается, но есть и сейчас. И тогда считалось, что программисты, делающие компиляторы, исчезнут, он будет генерироваться, потом, когда делали VDM, поняли, что от них никуда не денешься, надо лишь обеспечить методическую поддержку. ...
А вот RAISE появился, это уже где-то появился в 1985, первое серьёзне описание 1990, тогда же RSL, а первое серьёзное описание RAISE в публикациях 1993—95 годов. Понятно, что за эти 20—30 лет они постарались учесть ограничения подхода.
В рамках VDM естественно задумались о строгости, и перед тем как начинать анализ, корректна или некорректна программа, надо дать определение корректности. Есть идеи, какую программу можно назвать корректной? Если мат. модель создана, то считаем, что она сама по себе строгая, и корректность, её определение распределение на две части: дать матем. модель, и должен быть механизм для того, чтобы проверить, удовлетворяет ли реализация тем требованиям, которые сформулированы в модели.
Рассмотрим пример.
Мы уже не раз проходили, как устроена ОС, знаем, что процессы переходят из одних состояний в другие: например, iowait, пассивные. Это достаточно формальное определение, конечный автомат, и будем считать, что больше ничего нет. Микроядерная ОС (mm и pm) — порядка 10 строчек на С. Как проверить соответствие?
Например, проверить все переходы и состояния. Да, но этот подход недостаточно технологичный. Хотелось бы некое общее состояние получить.
Общий подход следующий: мы разделяем два мира: мир моделей и реализаций. В модели и реализации, и там и там, есть своё пространство составляющих. Для простоты будем считать, что есть операции, функции, и данные берутся из входного пространства данных и данные генерируются в выходное пространство данных. Эти пространства разные. И в случае модели есть такая структура данных, пис. конечный автомат. В программе реализации такой может не быть. Там могут быть структуры существенно более богатые. И имеются операции. И тогда для проверки корректности рисуется такая диаграмма: имеется некоторое состояние, и мы в этом состоянии i_model мы применяем к нему переход f_модель и получаем результат j_model. И можем сделать соответствие i_impl →(f_impl) j_impl. Заметьте, что, собственно, входные данные не просто разные, но и в разных пространствах лежат. Между ними надо и можно установить соответствие. Соответствие устанавливается в эту сторону. Это некое отображение от сложного к простому. Часто это отображение называют абстракцией. Более принятое название — функция retrieve, retr. Коротко и красиво что можно сказать: реализация корректна в том и только в том случае, если диаграмма коммутативна.
Эта функция необязательно должна быть тотальная, у неё есть что-то типа предусловия. Это отображение (f) определено, когда некое предусловие удовлетворяется. Заметьте, что в реализации пространстве оно тоже может быть. И это должно быть согласовано.
Для любого i в реализ. пространстве, если его retr удовлетворяет предусловию, то и оно сам должно ему удовлетворять.
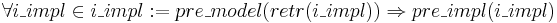
Почему не выполняется в другую сторону: пример с логарифмом
Этот подход в общем смысле формален, т.к.: предусловие может слаб. модель. По поводу постусловия обратная ситуация.
По поводу результирующих функций
Это хорошая самостоятельная работа.
Сейчас мы заканчиваем с VDM, после этого перейдём к RAISE.
Что реально нужно делать, чтобы доказывать корректность программ: RAISE очень похож на VDM. Спец. опис. реальным, рзм или имплицитным. Retr представляется как обычная функция, и потом просто нужно уметь доказывать, что два retr выполняются.
Был выдвинут тезис, что модель и retr должны быть адекватны, и это правильно. Но с другой стороны, если модель большая, то приходится сильнее абстрагироваться.
Основная сложность — в функции retr. Сложность retr фактически сложность реализации. Поэтому подход другой: строится цепочка моделей. Для компиляторов было порядка 5 или 6 этапов.
При помощи VDM верифицировали компилятор Ada.
Многие противники подхода говорили: вместо того, чтобы сделать работу честно и правильно 1 раз, необходимо сделать её несколько раз, провести работу по доказательству (которая очень трудоёмкая). Но опыт показал, что на компиляторах сроки разработки удаётся сократить и удаётся предъявить корректную программу с первого предъявления.
Товарищи, которые разработали VDM... RAISE расшифровывается как строгий подход к программной инженерии (rational approach to software engineering). Чтобы этим требованиям удовлетворять, самую сложную технологическую деталь в технологии VDM решили убрать — retr. Чем retr был хорош? Можно было изменять сигнатуру функции. VDM всё это разрешал, а RAISE запретил. что осталось? остался подход пошаговой детализации. Поскльку retr убрали, то сигнатуры модели и реализации совпали, структуры данных по существу одни и те же, т.к. что всё сильно упростилось, но при этом raise отошёл на ещё один шаг назад. Что было в VDM? Пусть в VDM первая модель — эксплицитная функция. При этом структуры данных должны быть описаны и заданы. В случае с нашим конечным автоматом разработчик может уже задуматься, как хранить состояние. Разработчики сказали, что на первом этапе модель должна быть предельно абстрактной. Функции есть, структур нет. И этот способ описания поведения системы, когда сигнатуры операций задаются, стр. не задаются, называют аксиоматической или алгебраической спецификацией. Есть тонкости в трактовке (кс и алг), но для нас разницы нет. В RAISE были введены аксиомы и при помощи них это опис.
И при помощи RAISE может расписать достаточно детально:
Из чего состоит технология RAISE: пис. модель нулевого уровня. Что должно быть задано?
0.1 Определяются некие типы данных. Не описываются, а просто объявляются. 0.2 Описываются сигнатуры операций (функций). Это значит, во-первых, задаётся имя функции и перечисляются типы операндов и результата (входных и выходных данных) 0.2.1 С точки зрения RAISE, константы это такая функция без значений Они указывают, что функция тотальна, детерминирована и терминирующ. Если функция нетотальная, то надо писать тильду. На уровне сигнатур в чём нетотальность определить нельзя, надо смотреть сигнатуру 0.3 Аксиомы.
Следующий шаг
1.1 Типы данных можно пополнить. 1.2 Можно пополнить набор функций. 1.3 Можно пополнить набор аксиом. Но все старые аксимы сохранятся. 1.4 Доказательство согласованности.
Модели 0 и 1 уровня должны быть согласованы. Как это делается. Согласованность с позиции RSL термин неформальный, а технология RAISE ... расматривается отношение уточнения, дана модель мдет уточн. другую, и мы можем считать что модель 1 уточняет модель 0, если одна уточняет другую. И уточняет, если всё сохраняется и добавлено только новое, и есть один нюанс, связанный с уточнением самих типов данных. До этого типы данных были представлены только именами, по мере того, как прибл. к реализации, мы в какой-то момент, не обязательно для всех типов одновременно, должны эти типы определить (списки, деревья....) переходят объявления к определению можно делать два раза, не более чем. Первый раз — берётся и пис. реальная структура (например T3 — натуральное число или T4 — список натуральных чисел). Могу уточнить (T4 — конечный список натуральных чисел). Это первое уточнение типа. Второй вид: для каждой стр. данных форм. определяется т. н. максимальный тип. Это некий тип., пр. природу. Для булевских чисел максимальных. типов вл. сами булевские числа. Для натуральных — целые. Для конечных списков, множеств, тобр — бесконечн. Если есть список натуральных чисел, то вопрос, что будет максимальным типом стр. данных, гр. список натуральных чисел? Бесконечный список целых чисел. Такое уточнение — максимизация — тоже правильное уточнение. Самое главное, что нужно доказать — все аксиомы сохраняются.
Техника доказательства достаточно простая и очевидная, как правило, подстановка. Дост.ю просто делать, если была аксиматическая спецификация, а в модели 1 написали определение. Помимо подст. исп. библиотек правил вывода, а она связ. с теориями, пстр. для типовых структур данных. Например: в случае множеств в теории сказано, что x ∈ {} всегда тождественно равно false. И при помощи последнего упрощения должны прийти к тому, что либо все аксиомы тождественно true, либо где-то не true, и вы доказали, что новая спецификация не является строгим уточнением исходной. В этом и состоит метод.
Пример: полностью пример имеется в методическом пособии.
Имеется схем, пис. БД
scheme DATABASE =
class type Database, Key, Data
value empty : Database,
insert : Key × Database → Database
remove : Key × Database → Database
defined : Key × Database → Bool
lookup : Key × Database → Data
axiom ∀ k : Key: - defined(K, empty) = false
Других ксим рассматривать не будем.
Эт нулевой уровень спецификации на первом обязаны пост. все спец. сигн, но БД, например, будет уточнена
type Database = (Key × Data) - set
value empty : Database = {}
defined : Ket × Database → Bool
defined()k,db = ∃ d : Data :- (k, d) ∈ db)
Проверяем. Все типы данных определены, все сигнатуры пр. Для одного типа данных сказали, что это мн-во пар, и для двух функций сказали, что empty всегда даёт пустое множество, и функция defined определена таким утверждением. Этого достаточно, чтобы рассуждать о сохранении или несохранении аксиомы. Для того, чтобы это делать, есть некая техника. В простом случае мы просто раскрываем все кванторы.
Раскрываем ∀, defined, empty, потом раскручиваем квантор существования и мы приходим к некоторому выражению: (k, d) ∈ {}. Мы знаем, что это false, это означает, что левая часть тождественно false, значит, аксиома тождественно true. Вот мы провели доказательство, что первая аксиома сохранилась.
Практик-еор сообр: как в общем случае проверять? общего ответа нет. Какие вообще спец. включать, а какие нет? В общем случае ответа на этот вопрос нет. Практический подход такой: в наших функциях мы делаем первое грубое разделение: какие функции сзд. новые данные в нашей системе (тут мы уже разделяем целевые объекты и вспомогательные). Те операции, где мы получаем новое состояние БД, это т.н. функции-генераторы, генераторы новых значений целевого типа. Те функции, которые позволяют узнать только некоторые характеристики, это некие обсерверы, которые позволяют что-то узнать (напр, lookup). Эти функции на состояние БД не влияют. И есть ещё более тонкое деление: функция remove. Любое значение Database мною построено при помощи цепочки инсертов, и для генерации всех значений БД куьщму не нужна, а а в реальной жизни нужна и в модели должна присутствовать. Эти функции, которые несут некоторую избыточность, их называют трансформерами или модификаторами. Они меняют состояние, но они приводят к состояниям, к которым можно без них перейти.
В число аксиом системы обычно включают аксиомы, описывающие генераторы и обсерверы. А после того, как отработал генератор или трансформер, как изменилось поведение системы? А это даёт обсервера. И если для комбинаторной генерации и обс. есть опис. поведение, то это даёт эффект генератора. Т.о., мы должны согласовать с лектором, это самое абсолютное описание системы, которое может быть.
Теперь грустном: на экзамене будет задача, на которой необходимо будет доказать правильности или неправильность уточнения.
По поводу реальной жизни: никакие подобные системы аналитически не заказываются, на отдельные подсистемы техника доказательства используется в RAISE. Тематика становится всё более востребованной.
Формальная спецификация и верификация программ
|
|


