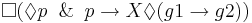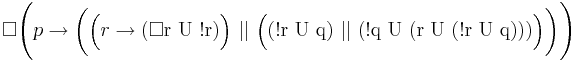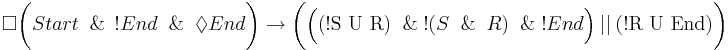ВПнМ, примеры задач/Задача 5
Материал из eSyr's wiki.
(→Задача 2 - преобразована в TeX) |
(→Вариант 3 - добвлена задача) |
||
| Строка 73: | Строка 73: | ||
== Вариант 3 == | == Вариант 3 == | ||
| - | |||
=== Задача 1 === | === Задача 1 === | ||
После события p и до наступления события q событие r наступает не более одного раза. (полученное свойство должно быть инвариантным к прореживанию) | После события p и до наступления события q событие r наступает не более одного раза. (полученное свойство должно быть инвариантным к прореживанию) | ||
| Строка 84: | Строка 83: | ||
#* до второго || — r встречается 0 раз | #* до второго || — r встречается 0 раз | ||
#* после второго || — r встречается 1 раз, записано с помощью трёх вложенных циклов (описание промежутков) | #* после второго || — r встречается 1 раз, записано с помощью трёх вложенных циклов (описание промежутков) | ||
| + | |||
=== Задача 2 === | === Задача 2 === | ||
| Строка 90: | Строка 90: | ||
<math>\Box \biggl( Start \And \ !End \And \Diamond End \biggr) \rightarrow \biggl( \Bigl( \text{(!S U R)} \And !(S \And R) \And !End \Bigr) \ || \ \text{(!R U End)} \biggr) </math> | <math>\Box \biggl( Start \And \ !End \And \Diamond End \biggr) \rightarrow \biggl( \Bigl( \text{(!S U R)} \And !(S \And R) \And !End \Bigr) \ || \ \text{(!R U End)} \biggr) </math> | ||
| + | |||
=== Задача 3 === | === Задача 3 === | ||
| + | В ходе итерации, начинающейся меткой START и заканчивающейся меткой END, выполнение оператора x==1 всегда влечет за собой приём сообщения, помеченного меткой S. | ||
| + | |||
| + | [] (START & !END & <>END -> ( (!P U END)||((P -> (!END U S))U END) ) | ||
| + | |||
| + | |||
| + | === Задача 4 === | ||
Пишите какие у вас задачи были. | Пишите какие у вас задачи были. | ||
| + | |||
{{Курс ВПнМ}} | {{Курс ВПнМ}} | ||
Версия 21:04, 24 мая 2009
Содержание[убрать] |
Вариант 1
Задача 1
После события 'процесс p находится на метке iter_begin' и до наступления события 'процесс p находится на метке iter_end' верно: сразу за событием 'значение глобальной переменной y равно 5' наступает событие 'значение глобальной переменной x равно 3' (полученное свойство не обязательно может быть инвариантным к прореживанию)
#define p_begin (p@iter_begin) #define p_end (p@iter_end) #define global5 (g==5) #define global3 (g==3)
[](<>p_begin && p_begin -> X <> (global5 -> X global3 ))
TeX'ом:
(по-моему, в формуле вообще нету p_end. такого быть не должно.)
Задача 2
До наступления события 'значение глобальной переменной state равно leave' верно: событие 'процесс p находится на метке sent' наступает не более одного раза
#define state_leave (state==leave) #define p_sent (p@sent)
[](p_sent -> X (!p_sent U state_leave))
Задача 3
Между событиями 'значение глобальной переменной state равно enter_critical' и 'значение глобальной переменной state равно leave_critical' верно: если наступило событие 'процесс p находится на метке lock', то до него было событие 'значение глобальной переменной state равно locked'
#define state_enter (state==enter_critical) #define state_leave (state==leave_critical) #define state_locked (state==locked) #define p_lock (p@lock)
[]( state_enter -> X((!p_lock U state_leave) || (<>p_lock && !p_lock U state_locked) )
Вариант 2
Задача 1
После наступления события 'значение глобальной переменной state равно enter_critical' верно: событие 'процесс q находится на метке received' наступает ровно один раз
#define S "state == enter_critical" #define was_received Q@received
[](S -> (<>was_received && [](was_received -> X([]!was_received))))
Задача 2
До наступления события 'значение глобальной переменной state равно leave' верно: событие 'процесс p находится на метке sent' наступает не менее одного раза
#define R "state == leave" #define was_sent P@sent
([]!R) || (!R U (was_sent && !R))
Задача 3
После события 'процесс p находится на метке iter_begin' и до наступления события 'процесс p находится на метке iter_end' верно: после события 'в канал c отправляется сообщение req' рано или поздно наступит событие 'из канала d принимается сообщение ack'
#define was_iter_begin P@iter_begin #define was_iter_end P@iter_end #define was_req ...@C_send_req #define was_ack ...@D_send_ack
[]((was_iter_begin) -> [](was_req -> (!was_iter_end U (was_ack && !was_iter_end))))
Вариант 3
Задача 1
После события p и до наступления события q событие r наступает не более одного раза. (полученное свойство должно быть инвариантным к прореживанию)
ps. пояснение формулы:
- до первого || — случай, когда q не факт, что произойдёт (после того, как произойдёт r, оно длится до тех пор, пока не прекратится)
- после первого || — случай, когда q обязательно произойдет
- до второго || — r встречается 0 раз
- после второго || — r встречается 1 раз, записано с помощью трёх вложенных циклов (описание промежутков)
Задача 2
В одной итерации вычисления между метками Start и End операция R всегда предшествует (не обязательно непосредственно) выполнению операции S (полученное свойство должно быть инвариантным к прореживанию).
Задача 3
В ходе итерации, начинающейся меткой START и заканчивающейся меткой END, выполнение оператора x==1 всегда влечет за собой приём сообщения, помеченного меткой S.
[] (START & !END & <>END -> ( (!P U END)||((P -> (!END U S))U END) )
Задача 4
Пишите какие у вас задачи были.