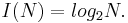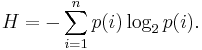ПОД: Ответы старые
Материал из eSyr's wiki.
(→Информация и её измерения.) |
(→Информация и её измерения.) |
||
| Строка 22: | Строка 22: | ||
Американский инженер Р. Хартли в 1928 г. процесс получения информации рассматривал как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определял как двоичный логарифм N. Формула Хартли: | Американский инженер Р. Хартли в 1928 г. процесс получения информации рассматривал как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определял как двоичный логарифм N. Формула Хартли: | ||
| - | : <math>I(N)= log_2 N.</math> | + | : <math>~I(N)= log_2 N.</math> |
| - | Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log_2 100 > 6,644. Таким образом, сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицы информации. | + | Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: <math>I = log_2 100 > 6,644</math>. Таким образом, сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицы информации. |
Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе. Формула Шеннона: | Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе. Формула Шеннона: | ||
: <math>H =-\sum_{i=1}^np(i)\log_2 p(i).</math> | : <math>H =-\sum_{i=1}^np(i)\log_2 p(i).</math> | ||
| - | где p_i — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений. | + | где <math>p_i</math> — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений. |
| - | Легко заметить, что если вероятности p_1, ..., p_N равны, то каждая из них равна 1 / N, и формула Шеннона превращается в формулу Хартли. | + | Легко заметить, что если вероятности <math>p_1, ..., p_N</math> равны, то каждая из них равна 1 / N, и формула Шеннона превращается в формулу Хартли. |
Помимо двух рассмотренных подходов к определению количества информации, существуют и другие. Важно помнить, что любые теоретические результаты применимы лишь к определённому кругу случаев, очерченному первоначальными допущениями. | Помимо двух рассмотренных подходов к определению количества информации, существуют и другие. Важно помнить, что любые теоретические результаты применимы лишь к определённому кругу случаев, очерченному первоначальными допущениями. | ||
Версия 18:37, 19 января 2010
Информация и её измерения.
Термин "информация" происходит от латинского слова "informatio", что означает сведения, разъяснения, изложение. Несмотря на широкое распространение этого термина, понятие информации является одним из самых дискуссионных в науке. В настоящее время наука пытается найти общие свойства и закономерности, присущие многогранному понятию информация, но пока это понятие во многом остается интуитивным и получает различные смысловые наполнения в различных отраслях человеческой деятельности: в обиходе информацией называют любые данные или сведения, которые кого-либо интересуют. Например, сообщение о каких-либо событиях, о чьей-либо деятельности и т.п. "Информировать" в этом смысле означает "сообщить нечто, неизвестное раньше"; в технике под информацией понимают сообщения, передаваемые в форме знаков или сигналов; в кибернетике под информацией понимает ту часть знаний, которая используется для ориентирования, активного действия, управления, т.е. в целях сохранения, совершенствования, развития системы (Н. Винер).
Клод Шеннон, американский учёный, заложивший основы теории информации — науки, изучающей процессы, связанные с передачей, приёмом, преобразованием и хранением информации, — рассматривает информацию как снятую неопределенность наших знаний о чем-то.
Приведем еще несколько определений: Информация — это сведения об объектах и явлениях окружающей среды, их параметрах, свойствах и состоянии, которые уменьшают имеющуюся о них степень неопределенности, неполноты знаний (Н.В. Макарова); Информация — это отрицание энтропии (Леон Бриллюэн); Информация — это мера сложности структур (Моль); Информация — это отраженное разнообразие (Урсул); Информация — это содержание процесса отражения (Тузов); Информация — это вероятность выбора (Яглом).
Современное научное представление об информации очень точно сформулировал Норберт Винер, "отец" кибернетики. А именно: Информация — это обозначение содержания, полученного из внешнего мира в процессе нашего приспособления к нему и приспособления к нему наших чувств.
Подходы к определению количества информации. Формулы Хартли и Шеннона.
Американский инженер Р. Хартли в 1928 г. процесс получения информации рассматривал как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определял как двоичный логарифм N. Формула Хартли:
Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log2100 > 6,644. Таким образом, сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицы информации.
Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе. Формула Шеннона:
где pi — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.
Легко заметить, что если вероятности p1,...,pN равны, то каждая из них равна 1 / N, и формула Шеннона превращается в формулу Хартли.
Помимо двух рассмотренных подходов к определению количества информации, существуют и другие. Важно помнить, что любые теоретические результаты применимы лишь к определённому кругу случаев, очерченному первоначальными допущениями.
В качестве единицы информации Клод Шеннон предложил принять один бит (англ. bit — binary digit — двоичная цифра). Бит в теории информации — количество информации, необходимое для различения двух равновероятных сообщений (типа "орел"—"решка", "чет"—"нечет" и т.п.).
В вычислительной технике битом называют наименьшую "порцию" памяти компьютера, необходимую для хранения одного из двух знаков "0" и "1", используемых для внутримашинного представления данных и команд.