МФСП: Оформление задач

Материал из eSyr's wiki.

Как показала практика, на коллоквиумах (и, вероятно, в какой-то степени на экзамене) придираются к оформлению задач. Здесь будут примеры, которые содержат необходимые формальности. Обращаю внимание, что это не мануал по решению и ботать но нему не стоит, это просто пример оформления.

Задача 5, метод Флойда

Условие

                START
          (y1, y2) = (0, x1)
                  |
   -------------->|
   |              B 
   |              |     T
   |           y2 >= x2-------
   |              |F         |
   |              |          |
(y1, y2) = (y1+1, y2-x2)     HALT: (z1, z2) = (y1, y2)

Предусловие: φ: x1 >= 0 /\ x2 > 0 Постусловие: ψ: x1 = x2*z1 + z2 /\ z1 < x2

Решение

1. Инвариант в B: P(x1, x2, y1, y2) is (x1 = x2*y1 + y2) /\ (y2 >= 0)

Имеем 3 пути:

• S-B

φ /\ (x1 >= 0) /\ (x2 > 0) /\ (y1 = 0) /\ (y2 = x1) => φ /\ (x1 = x2*y1 + y2) /\ (y2 >= 0)

• B-T-B

φ /\ (x1 = x2*y1 + y2) /\ (y2 >= 0) /\ (y2 >= x2) => φ /\ (x1 = x2*(y1+1) + (y2-x2)) /\ ((y2-x2) >= 0)

• B-F-H

φ /\ (x1 = x2*y1 + y2) /\ (y2 >= 0) /\ (y2 < x2) => φ /\ ((z1, z2) = (y1, y2)) /\ (x1 = x2*z1 + z2) /\ (z1 < x2)

2. Фундированное множество - (Nat, >), точка сечения B. Оценочная функция y2.

Условие корректности: φ /\ (x1 = x2*y1 + y2) /\ (y2 >= 0) => y2 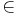Nat

Условие завершимости: φ /\ (x1 = x2*y1 + y2) /\ (y2 >= 0) /\ (y2 >= x2) => (y2 > y2-x2)