Основы Кибернетики, Алгоритмы решения задач/Задачи на синтез схем
Материал из eSyr's wiki.
[править] По заданной ФАЛ с помощью простейших методов, метода каскадов или метода Шеннона построить реализующую ее СФЭ или КС.
[править] Простейшие методы
[править] Промежуточные действия
- Если ФАЛ представлена в виде таблицы, то построим по ней совершенную ДНФ (как объединение всех возможных случаев, когда она равна 1).
- Если ФАЛ представлена в виде формулы, преобразуем ее, чтобы остались только функции базиса Б0. Кроме того, поднимаем все отрицания (они должны стоять только над переменными, но не над бо́льшими кусками выражения).
[править] Получение СФЭ
Строим как-нибудь подвыражения в соответствии с приоритетом операций. Поскольку оставлены только функции базиса Б0, то это не вызывает особых затруднений. Что вижу, то и рисую.
[править] Получение КС
Разбираем формулу
- A ∨ B преобразуем в ветвление, где один вариант реализует A, а другой — B
- A & B преобразуем в последовательное соединение, где первая часть реализует A, другая — B.
- xi преобразуем в контакт с меткой xi
- xi преобразуем в контакт с меткой xi
[править] Метод каскадов
[править] Промежуточные действия
Пусть у нас имеются булевы функции F1(x1, x2, … , xn), … , Fk(x1, x2, … , xn), зависящие от n переменных. Обозначим следующее множество:
M0 = {F1(x1, x2, … , xn), … , Fk(x1, x2, … , xn)}.
В простейшем случае, в нем одна функция. Воспользуемся следующим приемом:
F(x1, x2, … , xn) = x1*F(1,x2, … , xn)V x1*F(0, x2, …, xn)
Тогда определим правило построения следующих множеств (M1, M2, … , Mn):
Mi+1 = {g(0,xi+1, … , xn)|g∈Mi} U {g(1,xi+1, … , xn)|g∈Mi}.
Если функция представлена строкой значений, то формируем новое множество из левых и правых половин. Если функция представлена формулой, то подставляем в нее xi=0 и xi=1 и упрощаем. При этом после построения из Mi удаляются все фунции, несущественно зависящие от x1 (для строк значений это хорошо видно, т.к. левая и правая половина совпадает)
[править] Пример
f1(x1,x2,x3,x4)=(1000 0010 1111 1000) f2(x1,x2,x3,x4)=(1000 1111 0010 1000)
- M0 = {(1000 0010 1111 1000),(1000 1111 0010 1000)}
- M1 = {(1000 0010),(1111 1000),(1000 1111),(0010 1000)}
- M2 = {(1000),(0010),(1111)}
- M3 = {(10),
(00),(11)} - M4 = {0,1}
[править] Получение СФЭ
Реализуем на базе любого входа
- 0 = xi & xi
- 1 = xi V xi
Для реализации элемента Mi используем элементы Mi+1: пусть f(0,xi+1,...xn)=g(xi+1,...xn) и f(1,xi+1,...xn)=h(xi+1,...xn).
Тогда для реализации f соединеним дизъюнкцией конъюнкцию g и xi с конъюнкцией h и xi.
Реализацию элементов M0 метим как выходы СФЭ.
[править] Получение КС
Обозначаем все элементы всех множеств узлами КС.
- если g(xi+1,...xn)=h(0,xi+1,...xn), то соединим g и h контактом с меткой xi
- если g(xi+1,...xn)=h(1,xi+1,...xn), то соединим g и h контактом с меткой xi
После этого удаляем вершину с меткой 0 и все ведущие в нее контакты. Вершину с меткой 1, а также F1,...,Fk помечаем как входы КС.
[править] Метод Шеннона
[править] Промежуточные действия
Выбираем некоторое 1≤q≤n. Расклыдаваем исходное f(x',x") = V xi+1σi+1 & xi+2σi+2 & ... & xnσn & fσ"(x'). Обычно выбирают q = округленноый вниз(log2(n-2*log2(n))). После чего составляется универсальный многополюсник порядка q(имеющий q входов и 2n выходов) и мультиплексор порядка n-q (зависщий от адресных переменных xi+1, ... ,xn и от выходов универсального многополюсника, выдающий на выход fσ"(x') в соответствии с приведенной формулой в свой единственный выход).
Данный метод не применяется на практике для построения КС или СФЭ, это скорее мысленный эксперимент вроде падающего из окна Дэвида Дойча или квантового самоубийцы, используемый затем Шенноном и его последователями для оценки функции Шеннона...
[править] Получение СФЭ
Универсальный многополюсник в СФЭ выглядит так: Мультиплексор порядка q для f(x) в СФЭ выгладит так:
[править] Получение КС
Универсальный многополюсник в КС выглядит так: точно так же как в методе каскадов к каждой вершине приписываем x1 или x1, дабы соединить с новой волной вершин. В каждой следующем множестве будет в 2 раза больше вершин. Мультиплексор порядка q для f(x) в КС выгладит так:
[править] Оценить сверху или снизу сложность конкретной ФАЛ или сложность самой сложной ФАЛ из заданного множества в заданном классе схем.
[править] Оценка сложности самой сложной ФАЛ из класса
Для того, что посчитать сложность самой сложной ФАЛ из некоторого класса Q(n) ∈ P2(n), то есть, иначе говоря, вычислить функцию Шеннона, связанную с классом Q(n) (и для некоторого класса cхем U — например, СФЭ или КС), необходимо выполнить следующие шаги:
- Посчитать число функций в заданном классе Q(n).
- Сразу же из этого получить асимптотически нижнюю оценку функции Шеннона, связанной с классом Q(n):
- LK(Q(n)) ≳ log(|Q(n)|) / log(log(|Q(n)|))
- LC(Q(n)) ≳ log(|Q(n)|) / log(log(|Q(n)|))
- Показать, как для любой функции из данного класса построить схему из класса U, реализующую данную функцию и имеющую сложность, асимптотически равную вычисленной нижней оценке. Из этого будет следовать, что полученная асимптотически нижняя оценка является и асимптотически верхней оценкой, а из этого, в свою очередь, будет следовать, что функция Шеннона для заданного класса U(n) будет просто асимптотически равна полученной нижней оценке.
- В пункте 3 всегда пригождается следующее: для любой функции от n переменных можно построить, реализующую её СФЭ и КС со сложностью, асимптотически не превосходящей 2n / n
[править] Пример
- Посчитать функцию Шеннона, связанную с классом самодвойственных функций, для класса СФЭ.
- Самодвойственная функция f: f(x1, …, xn) = f(x1, …, xn)
Решение
- Первый пункт является самым главным. В нём нужно получить некоторую формулу, в которой любая функция из заданного класса выражается через функцию от меньшего числа переменных. Полученная формула пригодится и впоследствии. Например, для класса самодвойственных функций, разложим функцию f по первой переменной f(x1, x2, …, xn) = x1 & f(0, x2, …, xn) ∨ x1 & f(1, x2, …, xn) = x1 & f(0, x2, …, xn) ∨ x1 & f(0, x2, …, xn) = x1 & f0(x2, …, xn) ∨ x1 & f0(x2, …, xn), где f0 = f(0, x2, …, xn). Перепишем это в виде f(x1, …, xn) = x1 ⊕ f0(x2 ⊕ x1, …, xn ⊕ x1) (*). Теперь видно, самодвойственная функция от n переменных однозначно определяется функцией f0 от n − 1 переменной, и, следовательно, число самодвойственных функций от n переменных равно 22n − 1. В принципе, это и ежу очевидно, но полученная нами (*) потребуется нам в дальнейшем.
- Из пункта 1 следует что LC(Q(n)) ≳ 2n − 1 / n
- Из (*), а также из утверждения строим схему для произвольной самодвойственной функции. Строим f0 (сложность 2n − 1 / (n − 1)). Для n «⊕» потребуется ещё не более, чем C × n функциональных элементов. В итоге как раз и получится, что сложность результирующей схемы асимптотически не превосходит 2n − 1 / n
[править] Пример
- Посчитать функцию Шеннона, также для класса СФЭ, связанную с классом функций, таких, что:
f(x1, x2, x3, …, xn) = f(x3, x1, x2, …, xn)
Решение
- Разлагаем f по первым трём переменным:
- f(x1, x2, x3, x4, …, xn) = x1 & x2 & x3 & f(0, 0, 0, x4, …, xn) ∨ x1 & x2 & x3 & f(0, 0, 1, x4, …, xn) ∨ x1 & x2 & x3 & f(0, 1, 0, x4, …, xn) ∨ x1 & x2 & x3 & f(0, 1, 1, x4, …, xn) ∨ x1 & x2 & x3 & f(1, 0, 0, x4, …, xn) ∨ x1 & x2 & x3 & f(1, 0, 1, x4, …, xn) ∨ x1 & x2 & x3 & f(1, 1, 0, x4, …, xn) ∨ x1 & x2 & x3 & f(1, 1, 1, x4, …, xn) = (x1x2x3 ∨ x1x2x3) & fa ∨ ((x1x2x3 ∨ x1x2x3)) & fb (*),
где fa = f(0, 0, 0, x4, …, xn) = f(1, 0, 0, x4, …, xn) = f(1, 1, 0, x4, …, xn) = f(1, 1,1,x4,...,xn) = f(0, 1, 1, x4, …, xn) = f(0, 0, 1, x4, …, xn);
fb = f(0, 1, 0, x4, …, xn) = f(1, 0, 1, x4, …, xn). Теперь видно, что функция из данного класса однозначно определяется парой (fa, fb), где fa, fb — функции от n − 3 переменных. Таким образом, число функций из заданного класса равно числу таких пар, т. е. 22n − 3 × 22n − 3 = 22n − 2
- f(x1, x2, x3, x4, …, xn) = x1 & x2 & x3 & f(0, 0, 0, x4, …, xn) ∨ x1 & x2 & x3 & f(0, 0, 1, x4, …, xn) ∨ x1 & x2 & x3 & f(0, 1, 0, x4, …, xn) ∨ x1 & x2 & x3 & f(0, 1, 1, x4, …, xn) ∨ x1 & x2 & x3 & f(1, 0, 0, x4, …, xn) ∨ x1 & x2 & x3 & f(1, 0, 1, x4, …, xn) ∨ x1 & x2 & x3 & f(1, 1, 0, x4, …, xn) ∨ x1 & x2 & x3 & f(1, 1, 1, x4, …, xn) = (x1x2x3 ∨ x1x2x3) & fa ∨ ((x1x2x3 ∨ x1x2x3)) & fb (*),
- Из (1) следует, что LC(Q(n)) ≳ 2n − 2 / n
- Опять же, из (*) ясно, как строить схему для произвольной функции из заданного класса. Строим СФЭ для функций fa, fb (сложность каждой ≤ (2n − 3 / (n − 3)). И, кроме того, нам потребуется дополнительная константа С «∨», «&» и «¬» для реализации (*). Складывая (2n − 3 / (n − 3)) + (2n − 3 / (n − 3)) + С, получим как раз, что это ≲ 2n − 2 / n.
[править] Оценка снизу
[править] Оценка сложности ФАЛ
[править] Оценка сверху
[править] Оценка сложности самой сложной ФАЛ из класса
[править] Оценка снизу
[править] По заданной КС построить эквивалентную ей самокорректирующуюся КС.
[править] Определение самокорректирующейся КС
(p, q)-самокорректирующейся КС называют КС, из которой всегда получается эквивалентная ей КС (реализующая те же формулы через все контакты) после p операций обрыва контакта (смена проводимости одного контакта с xσ на 0) и q операций замыкания контакта (смена проводимости одного контакта с xσ на 1).
[править] Простейший способ построения
- Для защиты от одного разрыва каждый контакт заменяем на пару параллельных.
- Для защиты от n разрывов — на (n+1) дублирующих друг друга контактов.
- Для защиты от одного замыкания каждый контакт заменяем на пару последовательных.
- Для защиты от n замыканий — на (n+1) подряд идущих одинаковых контактов.
Итого, для (p, q)-самокорректирующей схемы мы каждый из контактов заменяем на последовательность из (q + 1) блоков, каждый из которых — параллельный пучок из (p + 1) контакта.
[править] Пример
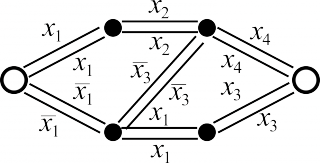
| Исходная контактная схема | Контактная схема, исправляющая один разрыв |
|---|---|
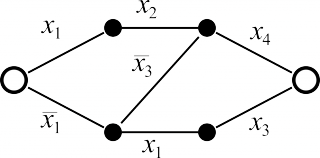
| 
|
| Контактная схема, исправляющая одно замыкание | Контактная схема, исправляющая один разрыв и одно замыкание |
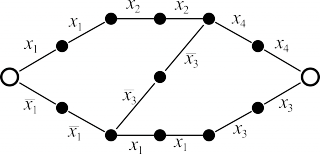
| 
|
[править] Способы с оптимизацией числа дуг самокорректирующейся КС
Существуют способы предварительной модификации схемы, после чего к контактам нетронутой части применяется описанный выше алгоритм.
[править] Для исправления одного замыкания
- Выделяем цикл из одинаковых контактов, вводим новую вершину и делаем ее центром звезды, на которую заменяем найденный цикл.
- Все контакты, не вошедшие ни в 1 цикл удваиваем последовательно.
- Данная конфигурация устойчива к одному замыканию, т.к. между любыми исходными узлами появляется не 1, а 2 контакта.
[править] Для исправления одного обрыва цепи
- Выделяем звезду из одинаковых контактов, удаляем все контакты звезды и соединяем все контакты циклом.
- Все контакты, не вошедшие ни в 1 звезду удваиваем параллельно.
- Данная конфигурация устойчива к одному обрыву, т.к. между любыми 2 узлами появляется не 1, а 2 пути.


